본 문서에서는 PLOS ONE 저널에 게재된 "Compressing Deep Graph Convolution Network with Multi-staged Knowledge Distillation" 논문을 소개합니다. 논문의 상세한 정보는 다음과 같습니다.
- Title: Compressing Deep Graph Convolution Network with Multi-staged Knowledge Distillation
- Authors: Junghun Kim, Jinhong Jung, and U Kang
- Journal: PLOS ONE (2021)
Node Classification
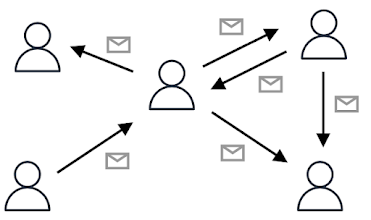
정점 분류(node classification)는 그래프에서 각 정점(node)을 분류하는 문제입니다. 예를 들어 카카오톡, 라인과 같은 메신저 네트워크에서 사용자끼리 메시지를 주고 받은 내역을 아래 그림과 같은 그래프로 모델링하여, 악성 사용자를 분류하는 문제 또한 정점 분류 문제입니다. 최근에 깊은 그래프 신경망(deep graph neural network)이 이 문제에서 좋은 성능을 보이며 주목받고 있습니다. 이는 그래프 신경망에서 레이어(layer) 수가 많아질수록 더 먼 거리의 정점으로부터 정보를 받아올 수 있어, 모델이 더욱 많은 정보를 활용할 수 있기 때문입니다. 그러나 그래프 신경망이 깊어질수록 학습해야 할 파라미터 수가 증가하고 모델의 크기는 커지게되어, 모바일이나 임베디드 시스템과 같은 제한된 컴퓨팅 리소스를 가지는 환경에서는 사용이 어렵습니다.
그림 1. SNS 네트워크에서 사용자끼리 주고 받은 메세지를 통해 생성한 그래프
Knowledge Distillation
지식 증류(knowledge distillation) 기법은 큰 모델을 작은 모델로 압축하여 제한된 컴퓨팅 리소스를 가지는 환경에서도 활용할 수 있도록 합니다. 이 기법은 간단한 방법으로 큰 모델의 성능을 작은 모델에서 보존할 수 있기 때문에 모델 압축 영역에서 널리 사용됩니다. 지식 증류 기법의 목적은 미리 잘 학습된 큰 모델(teacher model)의 지식을 실제로 사용하고자 하는 작은 모델(student model)에게 전달하여, 작은 모델로도 큰 모델과 비슷한 성능을 내는 것입니다. 따라서 큰 모델에서 어떠한 지식이 중요한지 판단하고, 이를 중점적으로 추출하여 작은 모델에게 효율적으로 전달해주는 것이 중요합니다.
먼 거리의 정점으로부터 정보를 받아와 더욱 많은 정보를 활용하여 모델의 성능을 높이는 다중홉 정보 확산(multi-hop message diffusion) 과정은 깊은 그래프 신경망의 핵심입니다. 하지만, 기존 지식 증류 기법들은 큰 모델을 압축할 때 다중홉 정보 확산 과정을 고려하지 않습니다. 따라서 기존의 지식 증류 기법들로 깊은 그래프 신경망을 압축하게 되면 성능 하락의 폭이 크다는 문제가 있습니다. 본 논문에서는 깊은 그래프 신경망(teacher model)의 다중홉 정보 확산 과정을 작은 그래프 신경망(student model)에서 보존하여, 기존 지식 증류 기법들의 성능을 향상시키는 Multi-staged knowledge Distillation(MustaD)를 제안합니다.
Proposed Method (MustaD)
본 논문에서 제안하는 MustaD는 큰 모델로부터 작은 모델에게 multi-staged knowledge를 증류하여 큰 그래프 신경망을 효과적으로 압축하는 기법입니다. 특히, 작은 그래프 신경망에서 깊은 그래프 신경망의 다중홉 정보 확산 과정을 보존하기 때문이, 깊은 그래프 신경망을 압축할 때 더욱 효과적으로 동작합니다. Multi-staged knowledge 지식 증류는 1) multi-hop feature aggregation 지식, 2) task prediction 지식의 두 단계에 거친 증류로 이루어져 있습니다. MustaD의 전체적인 구조는 그림 2와 같습니다.
그림 2. MustaD의 모델 구조
Multi-hop feature aggregation 지식은 그래프에서 먼 거리의 정점들로부터 정보를 취합하는 과정에 대한 지식으로, 이는 깊은 그래프 신경망들에서 가장 핵심적인 과정입니다. 깊은 그래프 신경망이 K 개의 그래프 신경망 레이어를 가지고 있다면, 이 모델은 K-홉(K-hop) 떨어진 정점들까지의 정보를 받아올 수 있습니다. 본 논문에서는 weight sharing 기법을 통해 Single Effective Layer로 K 개의 그래프 신경망 레이어를 모방합니다. 다시 말해, MustaD는 깊은 그래프 신경망(teacher model)의 다중홉 정보 확산 과정을 작은 그래프 신경망(student model)에서 단 한 개의 신경망 레이어로 모방합니다. 이에 더해 작은 그래프 신경망 레이어를 통과하여 나온 은닉 정점 임베딩(hidden node embeddings)이 깊은 그래프 신경망의 임베딩과 비슷해지도록 학습하여, 깊은 그래프 신경망의 다중홉 정보 취합 과정에 대한 지식을 증류합니다. 따라서 MustaD는 작은 그래프 신경망에서 깊은 그래프 신경망의 다중홉 정보 확산 과정을 보존하면서, 모델의 크기를 효과적으로 줄일 수 있습니다.
Task prediction 지식은 모델의 예측값에 대한 지식입니다. MustaD는 작은 그래프 신경망의 예측값이 큰 그래프 신경망의 예측값과 비슷해지도록 모델을 학습하면서 task prediction 지식을 증류합니다. 결론적으로 본 논문에서 제안된 MustaD는 multi-hop feature aggregation 지식에 더해 task prediction 지식을 추가적으로 증류시킴으로써, 성능 하락은 최소화하면서 깊은 그래프 신경망 모델을 효과적으로 압축합니다. 두 단계에 거친 지식 증류의 자세한 수식은 논문을 통해 확인할 수 있습니다.
Experiments
본 논문은 MustaD가 기존의 지식 증류 기반 모델 압축 기법들에 비해 더 높은 정확도를 달성한다는 것을 실험을 통해 보입니다. 그림 3은 세 개의 실세계 그래프 데이터에서 MustaD와 기존 기법들을 비교하는데, MustaD가 전체적으로 가장 좋은 성능을 보이고 있습니다. 특히 기존의 모델 압축 기법들은 teacher 모델의 그래프 신경망 레이어 수가 많아질 때 student 모델의 성능이 크게 변화하지 않는 반면, MustaD는 일관성 있게 student 모델의 정확도를 향상시킵니다. 이는 MustaD가 깊은 신경망 모델의 다중홉 정보 확산 과정을 효과적으로 보존하면서 큰 모델을 압축할 수 있다는 것을 보여줍니다.
그림 3. 세 개의 데이터셋에서 MustaD와 기존 알고리즘의 정점 분류 정확도 비교
Conclusion
본 문서에서는 PLOS ONE 저널에 게재된 "Compressing Deep Graph Convolution Network with Multi-staged Knowledge Distillation" 논문에 대해 소개하였습니다. 해당 논문은 두 단계에 거친 지식 증류를 통해 깊은 그래프 신경망을 효과적으로 압축하는 MustaD 기법을 제안하였습니다. 실세계의 데이터에서 실험을 진행한 결과, MustaD가 기존의 압축 방법들보다 정점 분류 문제에서 더 높은 분류 정확도를 보인다는 것을 보였습니다.
최근 그래프 신경망 분야에서 높은 정확도를 달성한 여러 깊은 그래프 신경망들은 모델의 크기가 커서 컴퓨팅 리소스가 부족한 환경에서는 사용이 어려웠습니다. 본 논문에서 제안된 MustaD는 깊은 그래프 신경망의 성능을 보존하면서 모델의 크기를 효과적으로 압축할 수 있습니다. 이에 따라 기존의 깊은 그래프 신경망들을 스마트폰, IoT 장치 등의 제한된 컴퓨팅 자원을 가지는 환경에서도 사용할 수 있게하여, 깊은 그래프 신경망의 활용 가능 범위를 확장합니다. 자세한 내용은 논문에서 확인할 수 있습니다 (링크).